Bookmakers close, or severely limit, accounts and even the world’s largest betting exchange has found it necessary to introduce a Premium Charge, implicitly acknowledging that a number of people have the ability to consistently identify favourable bets and the discipline to bet only, or perhaps mostly, when it is value for them to do so.
What Is The Kelly Staking Strategy?
If the goal of all punters is to grow their bankrolls as optimally as possible, what is the best staking strategy to help us achieve this goal?
It’s the subject of much debate, but the answer to this is that stakes should be calculated according to the Kelly Criterion. Why? Because the Kelly Criterion seeks to calculate the optimum stake for any value bet so as to maximise that value as well as maximise the growth of your betting bankroll. In other words, the Kelly Criterion takes into account both the size of your advantage (I.e the value available) and the size of your bankroll, so as to minimise risk and maximise your advantage.
When this solution is applied in the field of sports investing however, there are a number of challenges.
Issues With The Kelly Criterion & The Optimal Strategy
As John Larry Kelly Junior’s original 1956 paper makes clear (you can read it here), the criterion is only valid “when the investment or ‘game’ is played many times over, with the same probability of winning or losing each time, and the same payout ratio”.
This is unfortunate. In the world of sports, no two events are ever exactly the same. Bet on red on the roulette wheel and you know exactly what the probability is, but since the edge in casinos is in favour of the house, the Kelly Criterion isn’t going to help you here.
For Kelly to work, you must have a positive edge, a value opportunity. If the edge is precisely zero, the Kelly Criterion recommends no bet be placed, and of course if the edge is negative, again there is no bet.
So how can the Kelly Criterion help in the real world of sports, where precise probabilities are not known?
To help answer this, let’s take a simple example of a game where the true probability is 50%, but the payout exceeds this. You have a value bet, but it should be obvious that betting the full bank each time is not the best way to approach this. Your chances of going bust are extremely high.
At the other end of the risk spectrum is the ultra-cautious approach of staking a small fraction of the bank each time. While the chances of going bust are now very small, your bank isn’t going to grow very fast.
Clearly the optimal strategy lies between these two extremes, and Kelly calculated that the fraction of the bank to be staked equals the size of your edge. For example, if the chance of a win is 51%, and the price available is evens, you should bet your edge of 2% (51% -49%), 49% being the probability of losing. If you have a bigger edge, for example your chance of a win is 53%, your stake should be 6% (53% – 47%).
Kelly Criterion Calculator
To see the formula in action, lets take an example of a football match where the odds available on the draw are 3.50 (or 5/2 with an implied probability of 28.6%) but your estimate of the true probability is 30%.
The formula for calculating the Kelly stake is:
| [(Probability multiplied by odds) – 1] divided by (odds-1). |
Thus Kelly stake:
| [(0.3 * 3.50) – 1] / (3.50 – 1) | |
| [(0.3 * 3.50) – 1] / 2.5 | |
| [1.05 – 1] / 2.5 | |
| 0.05 / 2.5 | |
| 0.02, i.e. the stake should be 2% of the bank. |
The Kelly Staking Formula
To see the Kelly formula in action, let’s take an example of a football match where the odds available on the draw are 3.50 (or 5/2 with an implied probability of 28.6%) but your estimate of the ‘true’ probability of the draw is 30%.
The formula for calculating the Kelly stake is:
[(Probability multiplied by odds) – 1] divided by (odds-1)
Thus the Kelly stake is calculated as:
= [(0.3 * 3.50) – 1] / (3.50 – 1) =[(0.3 * 3.50) – 1] / 2.5 =[1.05 – 1] / 2.5 =0.05 / 2.5 =0.02
In this example, we should place 2% of our bankroll on this bet. If our bankroll is £1000, then our bet stake should be £20.
Fractional Kelly Staking Calculator
When applying Kelly, the consequences of over-estimating your edge are serious, and as we mentioned earlier, in sports the probability of an outcome is imprecise. It is for this reason that most punters err on the side of caution, and use the more cautious strategy of ‘fractional Kelly’. This means that rather than bet the suggested percentage, you use a fraction of it, commonly a half (Half-Kelly) but it can be any fraction.
How are fractional Kelly Stakes calculated? It’s fairly simple:
(((Probability multiplied by odds) – 1) divided by (odds – 1)) multiplied by your chosen fraction
So if we were to apply a Half Kelly staking strategy to our previous example, the Kelly Stake is calculated as:
= ((((0.3 * 3.50) – 1) / (3.50 -1)) * 0.50 = (((0.3 * 3.50) – 1] / 2.50) * 0.50 =((1.05 – 1] / 2.50) * 0.50 =(0.05 / 2.50) * 0.50 = 0.02 * 0.50 = 0.01
So in this example, applying a Half Kelly staking strategy would recommend betting 1% of our bankroll on this particular bet. So if our bankroll is £1000, then our stake should be £10.
You can apply any fraction you like. We particularly recommend betting a 10% Kelly strategy. It is somewhat conservative, but it allows you to diversify your betting, placing numerous bets on any given day, while minimising risk. You can read more about this approach here. This is a sensible way of handling the inevitable losing runs which occur, even if you have a favourable bet. Your bank will increase in the long run, only more slowly, but the risk of blowing the bank are reduced.
Progress and bank balance will not be a smooth upward slope and will be interrupted by frequent drawbacks (losing runs) but by using the Half-Kelly bet, volatility is greatly reduced, yet returns 3/4 of the compound return. For many gamblers, that is a price worth paying.
It can be shown that a Kelly bettor has a 1/2 chance of halving a bankroll before doubling it, and that you have a 1/n chance or reducing your bankroll to 1/n at some point in the future. For comparison, a Half Kelly bettor only has a 1/9 chance of halving their bankroll before doubling it.
Kelly Criterion Excel Spreadsheet
We’ve developed a Kelly Criterion formula Excel spreadsheet that you can download here. It’s free and easy to use. Simply input your betting bankroll, the odds on offer, your assessed probability for that outcome occurring and your Kelly fraction. Our Kelly Criterion Excel spreadsheet will calculate the optimum stake for your bet.
Kelly Staking Football Excel Spreadsheet
We’ve also developed a Kelly formula Excel spreadsheet for 1X2 football betting. Simply enter the teams, their odds, your assessed probability of each result (win or draw) as well as your betting bankroll and preferred Kelly fraction, and the Kelly football calculator will tell you exactly how much you should bet on each result this weekend.
How To Make Your Own Kelly Calculator In Excel
Creating your own Kelly staking calculator in an Excel spreadsheet is fairly simple. Here’s how you do it.
Step 1
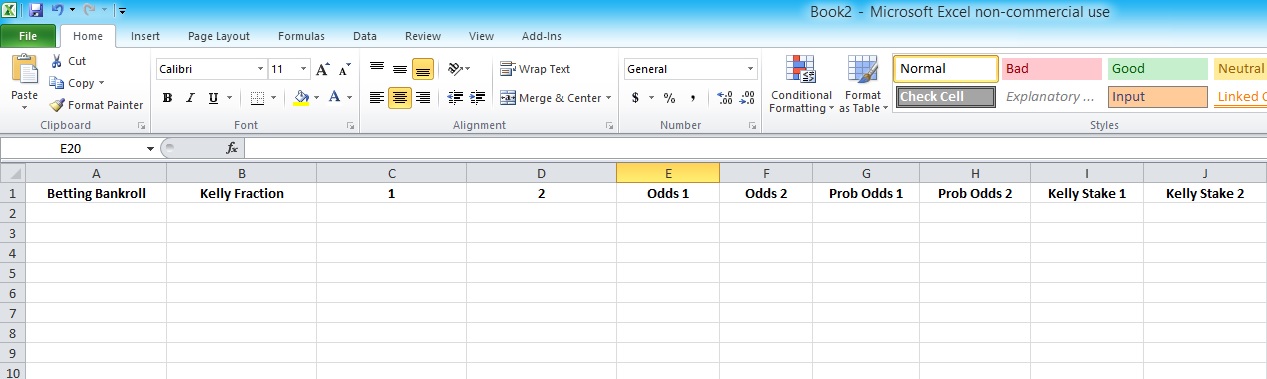
Open a new Excel spreadsheet and create the following headers: Betting Bankroll, Kelly Staking Fraction, 1 (outcome 1), 2 (outcome 2), Odds 1, Odds 2, Probability of 1, Probability of 2, Kelly Stake 1 and Kelly Stake 2
Then click the centre align button to ensure all data is displayed in the centre of their cells.
This is what you get:
Step 2
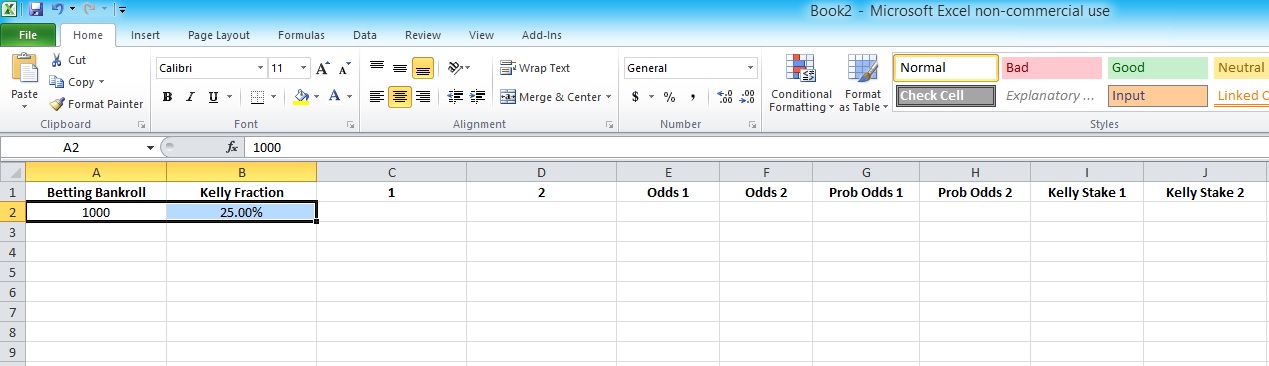
Enter both your current betting bankroll and your preferred Kelly staking fraction into the cells accordingly.
Step 3
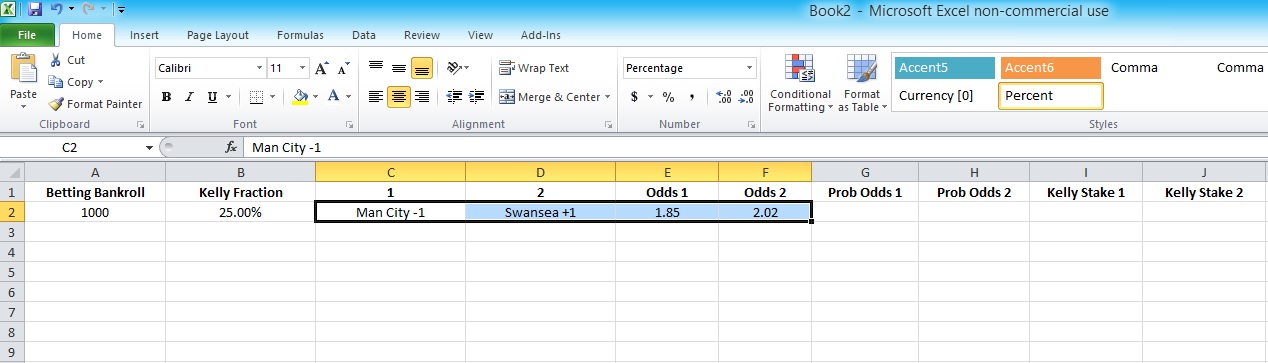
Next enter the two possible outcomes for this market and the odds on offer for each outcome. In this example we are betting on the Asian Handicap in a Premier League match between Manchester City and Swansea.
Step 4
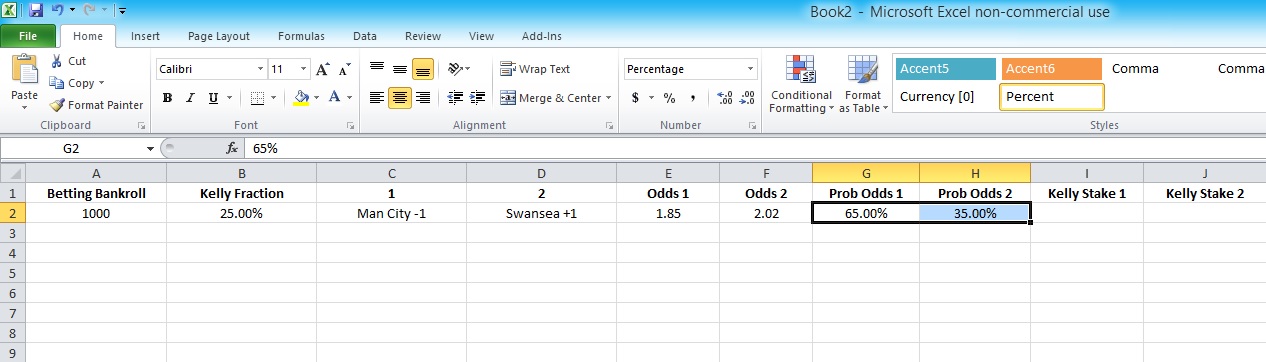
Next enter your assessed probability for each outcome occurring.
Step 5
Now we get down to the serious business. In cell I2 add the following formula:
=((((E2*G2)-1)/(E2-1))*A2)*B2
In this case…
E2 = odds for outcome 1
G2 = your assessed probability for outcome 1
A2 = your current betting bankroll
B2 = your preferred Kelly staking fraction
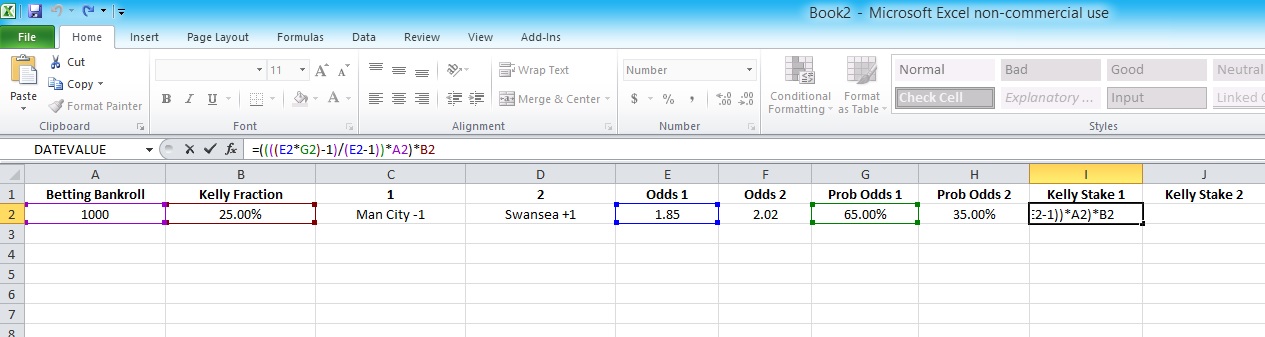
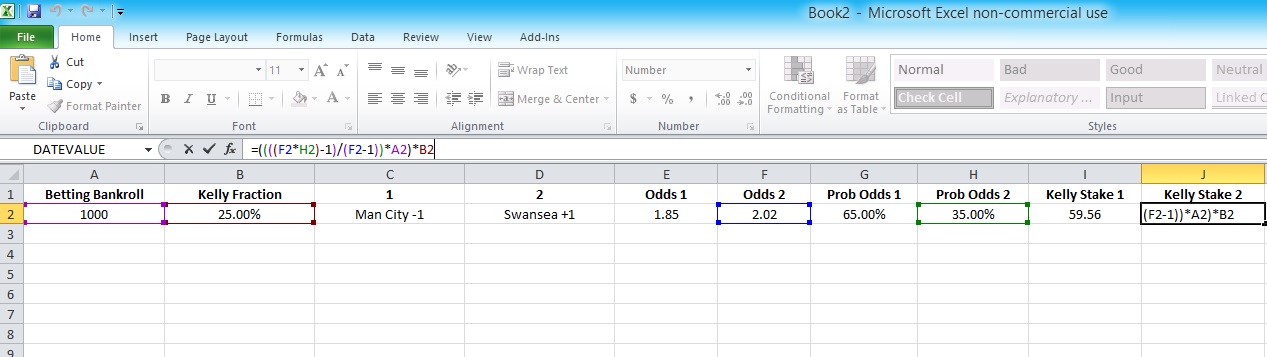
And in cell j2 add the following formula:
=((((F2*H2)-1)/(F2-1))*A2)*B2
In this case…
F2 = odds for outcome 2
H2 = your assessed probability for outcome 2
A2 = your current betting bankroll
B2 = your preferred Kelly staking fraction
You’re done. The spreadsheet will now tell you how much to bet on any given market. (When the suggested Kelly Stake is less than 0, it means no bet is advised.)
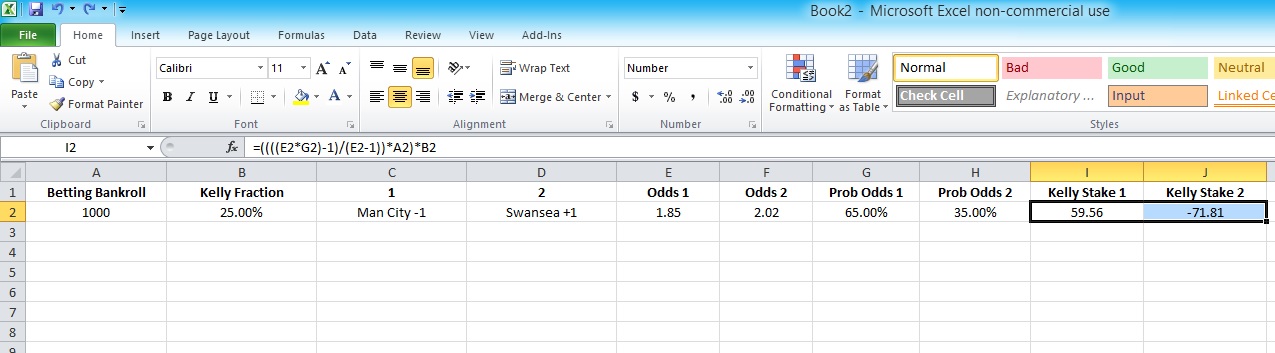
In our example, the calculator is recommending we bet £59.56 of our £1000 bankroll on Manchester City -1 goal at odds of 1.85.
The Benefits Of Using Kelly Staking
Progress and bank balance will not be a smooth upward slope, and will be interrupted by frequent drawbacks (losing runs) but by using the fractional Kelly approach, volatility is greatly reduced, yet returns 3/4 of the compound return. For many gamblers, that is a price worth paying.
Why is a more conservative approached better? Using the Full Kelly, an average punter has about a 33% chance of seeing their bankroll cut in half before that bankroll will be doubled. Applying a more conservative approach, such as the Half Kelly, the average punter has about an 11% chance of seeing their bankroll cut in half before it they see it doubled.
